Fortune's algorithm
Fortune's algorithm is a sweep line algorithm for generating a Voronoi diagram from a set of points in a plane using O(n log n) time and O(n) space.[1][2] It was originally published by Steven Fortune in 1986 in his paper "A sweepline algorithm for Voronoi diagrams."[3]
Contents |
Algorithm description
The algorithm maintains both a sweep line and a beach line, which both move through the plane as the algorithm progresses. The sweep line is a straight line, which we may by convention assume to be vertical and moving left to right across the plane. At any time during the algorithm, the input points left of the sweep line will have been incorporated into the Voronoi diagram, while the points right of the sweep line will not have been considered yet. The beach line is not a line, but a complex curve to the left of the sweep line, composed of pieces of parabolas; it divides the portion of the plane within which the Voronoi diagram can be known, regardless of what other points might be right of the sweep line, from the rest of the plane. For each point left of the sweep line, one can define a parabola of points equidistant from that point and from the sweep line; the beach line is the boundary of the union of these parabolas. As the sweep line progresses, the vertices of the beach line, at which two parabolas cross, trace out the edges of the Voronoi diagram.
The algorithm maintains as data structures a binary search tree describing the combinatorial structure of the beach line, and a priority queue listing potential future events that could change the beach line structure. These events include the addition of another parabola to the beach line (when the sweep line crosses another input point) and the removal of a curve from the beach line (when the sweep line becomes tangent to a circle through some three input points whose parabolas form consecutive segments of the beach line). Each such event may be prioritized by the x-coordinate of the sweep line at the point the event occurs. The algorithm itself then consists of repeatedly removing the next event from the priority queue, finding the changes the event causes in the beach line, and updating the data structures. As there are O(n) events to process (each being associated with some feature of the Voronoi diagram) and O(log n) time to process an event (each consisting of a constant number of binary search tree and priority queue operations) the total time is O(n log n).
Pseudocode
Pseudocode description of algorithm [4]
Note: This pseudocode uses a horizontal sweepline and not vertical as in the above example.
letbe the transformation
, where
is a parabola with minimum at
let T be the "beach line" let
be the region covered by site p. let
be the boundary ray between sites
and
. let
be the sites with minimal
-coordinate, ordered by
-coordinate
create initial vertical boundary rays
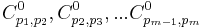
while not IsEmpty(
) do
← DeleteMin(
) case
of
is a site in
: find the occurrence of a region
in
containing
, bracketed by
on the left and
on the right create new boundary rays
and
with bases
replace
with
in
delete from
any intersection between
and
insert into
any intersection between
and
insert into
any intersection between
and
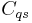
is a Voronoi vertex in
: let
be the intersection of
on the left and
on the right let
be the left neighbor of
and let
be the right neighbor of
in
create a new boundary ray
if
, or create
if
is right of the higher of
and
, otherwise create
replace
with newly created
in
delete from
any intersection between
and
delete from
any intersection between
and
insert into
any intersection between
and
insert into
any intersection between
and
record
as the summit of
and
and the base of
output the boundary segments
and
endcase endwhile output the remaining boundary rays in

Weighted sites and disks
As Fortune describes in [1] a modified version of the sweepline algorithm can be used to construct an additively weighted Voronoi diagram, in which the distance to each site is offset by the weight of the site; this may equivalently be viewed as a Voronoi diagram of a set of disks, centered at the sites with radius equal to the weight of the site.
Weighted sites may be used to control the areas of the Voronoi cells when using Voronoi diagrams to construct treemaps. In an additively weighted Voronoi diagram, the bisector between sites is in general a hyperbola, in contrast to unweighted Voronoi diagrams and power diagrams of disks for which it is a straight line.
References
- ^ a b Mark de Berg, Marc van Kreveld, Mark Overmars, and Otfried Schwarzkopf (2000), Computational Geometry (2nd revised ed.), Springer-Verlag, ISBN 3-540-65620-0 Section 7.2: Computing the Voronoi Diagram: pp.151–160.
- ^ Austin, David, Voronoi Diagrams and a Day at the Beach, Feature Column, American Mathematical Society, http://www.ams.org/featurecolumn/archive/voronoi.html.
- ^ Steven Fortune. A sweepline algorithm for Voronoi diagrams. Proceedings of the second annual symposium on Computational geometry. Yorktown Heights, New York, United States, pp.313–322. 1986. ISBN 0-89791-194-6. ACM Digital LibrarySpringerLink
- ^ Kenny Wong, Hausi A. Müller, An Efficient Implementation of Fortune's Plane-Sweep Algorithm for Voronoi Diagrams, http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.83.5571.